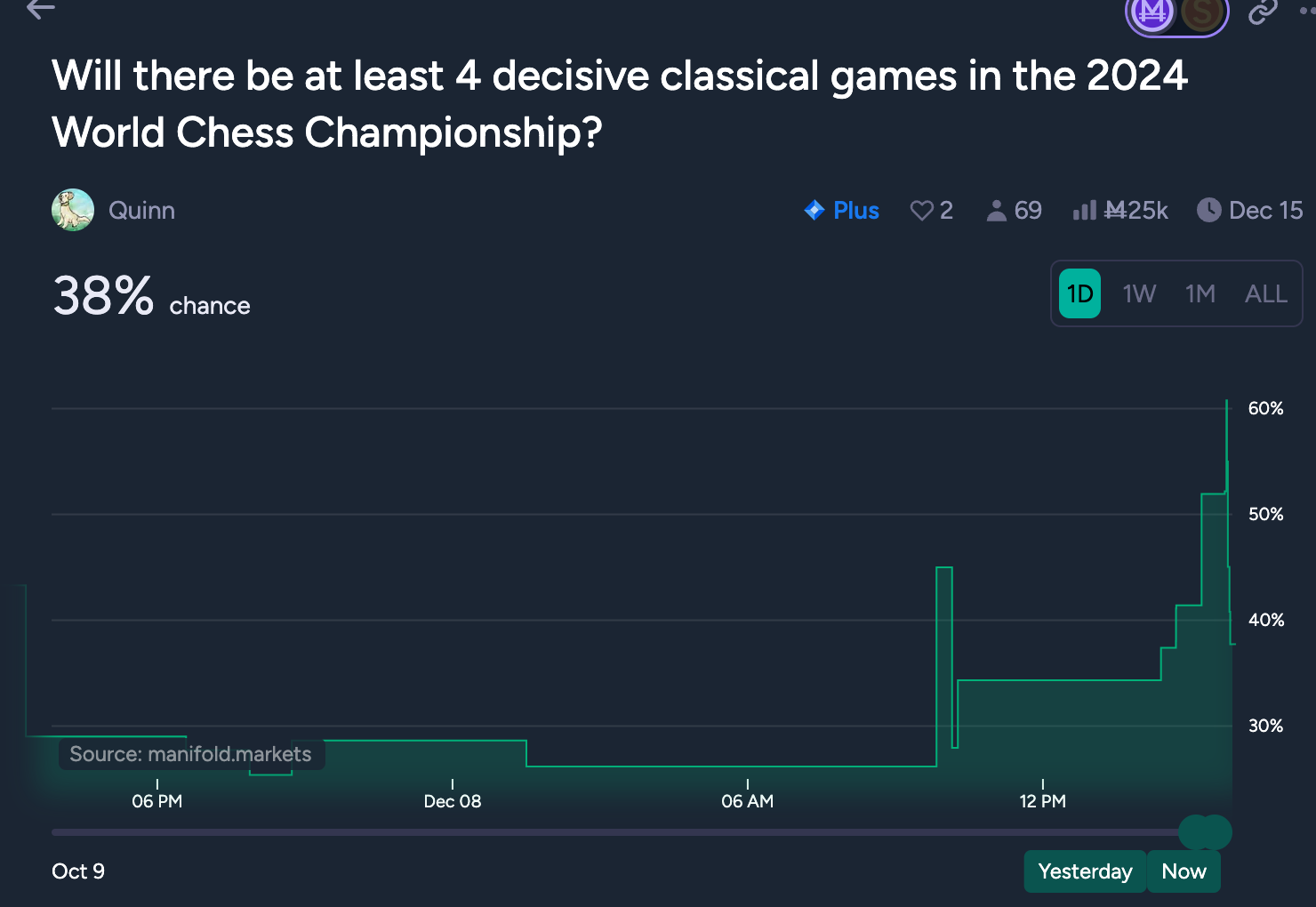
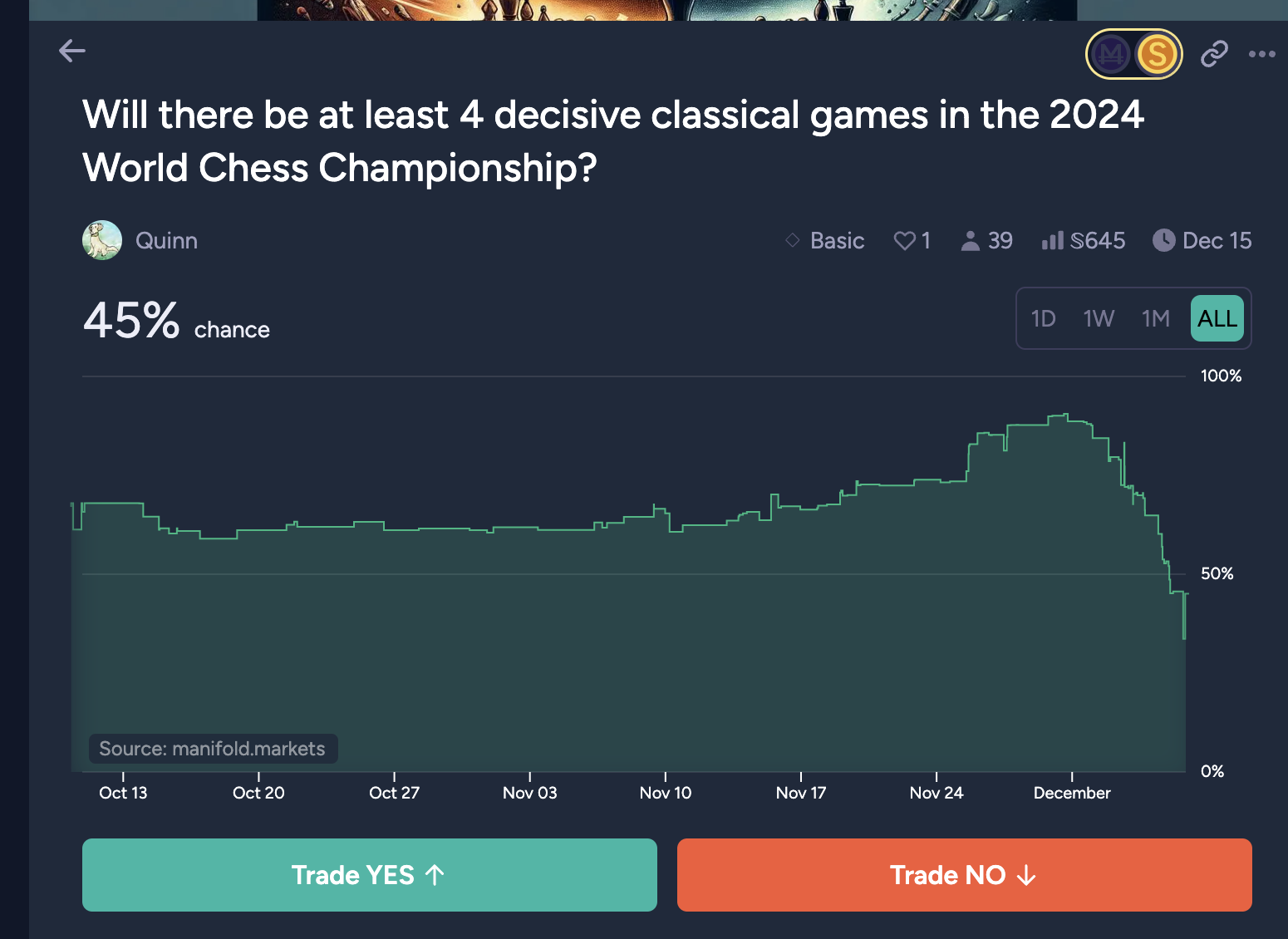
Resolves YES if there are four or more decisive (non-drawn) games in the classical (not including tiebreaks) portion of the World Chess Championship (https://en.wikipedia.org/wiki/World_Chess_Championship_2024), or NO if there are three or less. Also resolves NO if a new world chess championship does not start before 2025. (i.e. if the existing match is cancelled.)
Decisive game count for previous recent WCCs:
2023: 6
2021: 4
2018: 0
2016: 2
2014: 4
2013: 3
@diracdeltafunk hardly...this has been a long con by Gukesh to raise interest and viewership in a match which would have been very boring otherwise. I have it on good info that he is finally serious about things ready to polish off Ding decisively in the last few rounds.
@diracdeltafunk this is still the freest money i have ever seen in my life. If i could bet on sweepcash markets i would put all my earthly possessions here
@diracdeltafunk I mean it doesn't take much conviction to think this lol...if this was football, Gukesh and Ding would be underperforming their xG by a lot, considering they both have blown >80% win positions 3 times. That can't last forever (it can, but likely not). At any rate, even if i end up wrong, one player will certainly win a game soon, and this market will go to 75% and you can sell at a profit
Interesting.
It all depends on what you think the likelihood of a draw is.
If you say 70%
After Game 10:
2 (70%) - 3 (30%)
After Game 11:
2 (49%) - 3 (42%) - 4+ (9% - YES)
After Game 12:
2 (34.3%) - 3 (44.1%) - 4+ (21.6% - YES)
After Game 13:
2 (24.0% - NO) - 3 (41.2%) - 4+ (34.8% - YES)
After Game 14:
2 (16.8% - NO) - 3 (36.0% - NO) - 4+ (47.2% - YES)
@dlin007 while I think this is a little bit of a martingale strategy:
"At any rate, even if i end up wrong, one player will certainly win a game soon, and this market will go to 75% and you can sell at a profit"
I do think you're probably directionally correct for a different reason:
If there's one decisive game over the next three games, the odds that the losing player will then have to play for a win in the last game goes up dramatically.
For the same reason, @ChinmayTheMathGuy that analysis is nonsense. The odds of there being just 1 decisive result in the last 5 games (vs 0 or 2+) is much lower than you'd calculate from those odds
@benshindel must-win games seem to have a weirdly high draw rate, compared to what you would expect-i.e, look at the last round of the candidates.
dawg it's just a framework to analyze this market by looking at the state game by game. I noted that the draw rate is biggest factor to finding the "true odds" of this market.
in a 2 person match a must-win for one player is a must-draw for the other and we know Ding loves draws and Gukesh struggles to convert small edges.
Feel free to adjust the probabilities as you see them, but I didn't want to add additional assumptions beyond the 70% draw rate (which is supported by prices on polymarket).
if you claim the analysis is incorrect (which I'm open to, how does the draw rate change from the baseline 70%.
Do you think the probability of 5 more draws is different than 70%⁵= 16.8%?
I doubt it could be much higher since there's a minimum entropy in 2700 rated chess (barring collusion) compared to 3700 rated chess which is nearly 0 entropy from the starting position.
Potentially lower if one player thinks they are an underdog in the tiebreak. But still 70% seems fair considering how the last 6 games all draws with Gukesh pushing and Ding offering repetitions.
for 2+ wins, do you think the odds of a draw decrease to 60% given a player has a 1 pt advantage?
If so here's the updated analysis
After Game 10:
2 (70%) - 3 (30%)
After Game 11:
2 (49%) - 3 (39%) - 4+ (12% - YES)
After Game 12:
2 (34.3%) - 3 (38.1%) - 4+ (27.6% - YES)
After Game 13:
2 (24.0% - NO) - 3 (33.2%) - 4+ (42.8% - YES)
After Game 14:
2 (16.8% - NO) - 3 (27.1% - NO) - 4+ (56.1% - YES)
As I've said before, I know what I'm talking about, I don't post "nonsense" comments.
It seems like you just like dismissing legit analysis for not being sophisticated enough instead of understanding I'm just posting baseline numbers that can easily be updated by adding more degrees of freedom to the toy model.
re: xG
I'm not a soccer (football) fan but I don't really understand the appeal of xG as a predictive tool.
It's essentially a "what if score" that relies on a black box ML model to regress the variance in shot making to an arbitrary "mean" shot making rate. To me it makes more sense to look at the actual results and update your priors accordingly.
They tried doing shotQuality scores for the NBA a couple years back, but it didn't really catch on.
Not sure how you'd use the xG framework for chess, but I guess you're talking about missed chances to convert +1 advantages to wins.
But one player's failure to convert is the other player's ability to defend, so perhaps there being 3 draws where a player had a 80% chance of winning means you'd expect more than 2 wins so far, but it also means the markets were miscalibrated since the players said they didn't see the win in their post game press conference.
so in terms of updating the probability of a draw as we get match results. When 2 of 3 games were decisive the odds of a draw were in the 55-60% range but now with 6 straight draws it's up to ~70%.