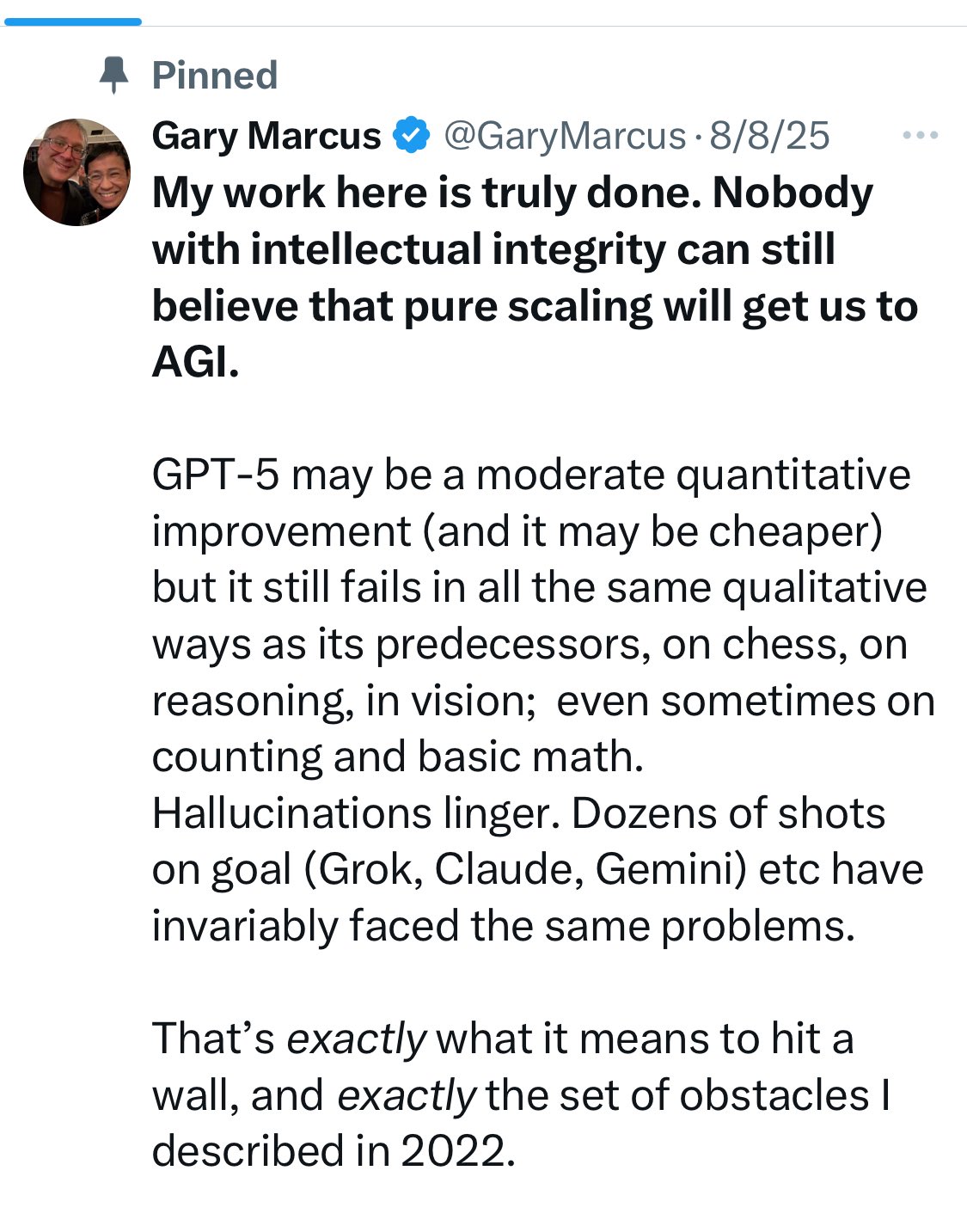
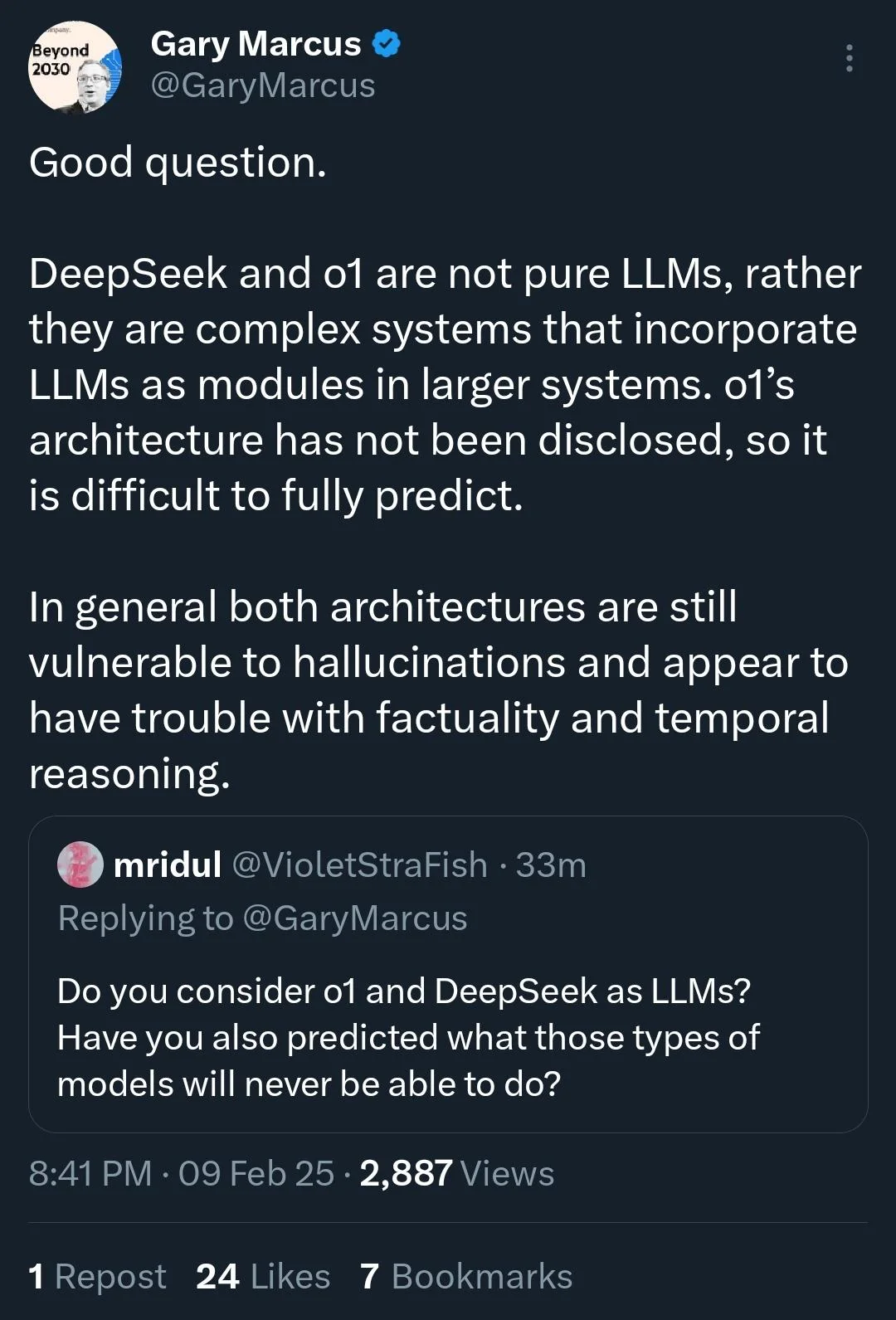
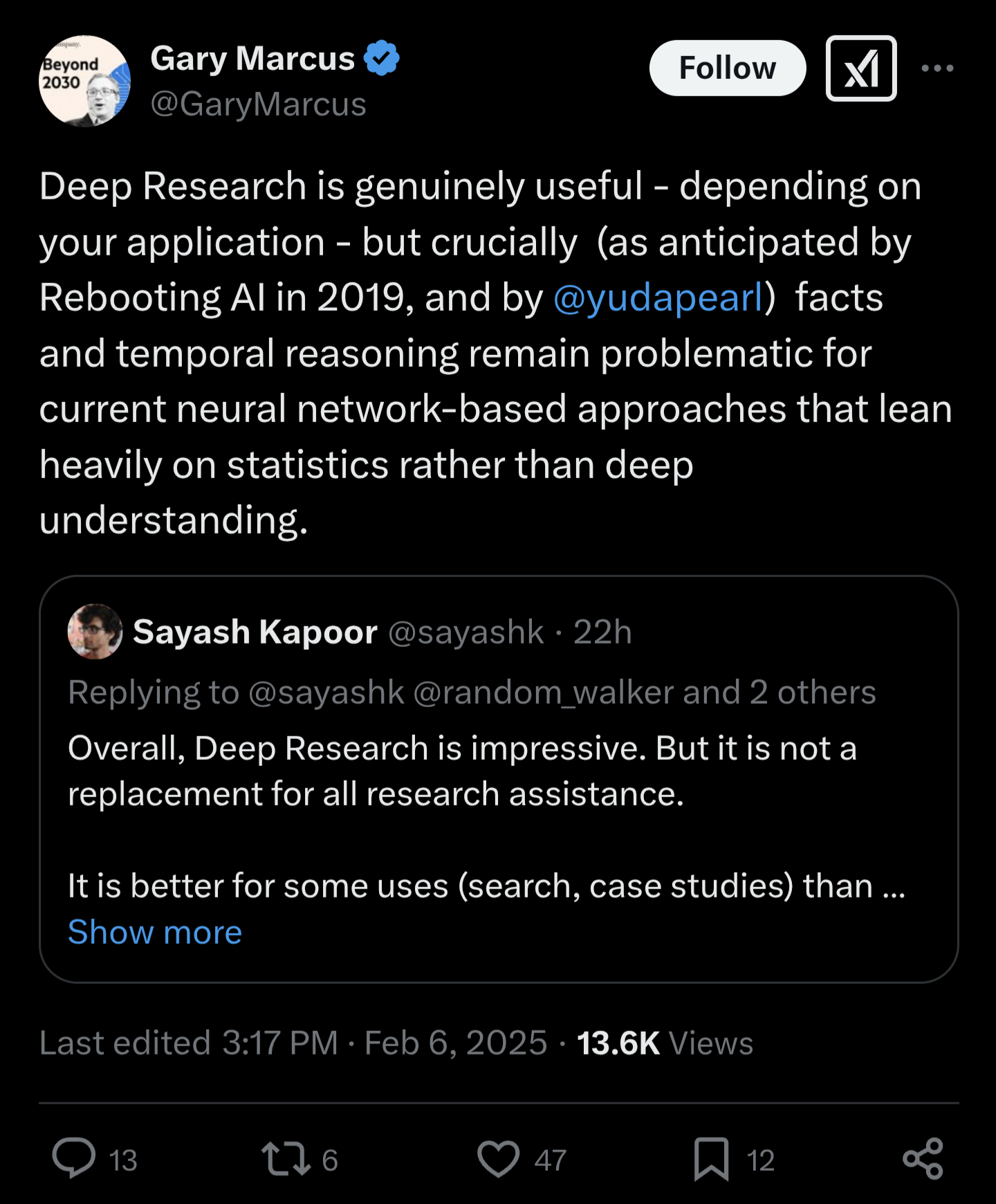
Resolves as YES if there is strong evidence that Gary Marcus has made a public statement suggesting that deep learning models are not capable of reasoning after a valid proof of the Riemann hypothesis has been made public. The underlying mathematics of this proof must have been generated/discovered by an AI system which leverages deep learning as one of its core mechanisms. Limited human authorship on top of the AI-discovered proof regarding the original publication is permissible provided this extends only to things such as formatting, ordering and explanations of various steps.

This must take place before January 1st 2050 in order for this question to resolve as YES. If a qualifying proof is made public, and Gary Marcus makes such a statement between the time of publication and the time when the proof is broadly considered as being valid by the mathematics community, then this question resolves YES (provided that this proof becomes considered valid before 2050). If no such credible proof is published before January 1st 2050, then this question resolves as NO. If Gary Marcus stops making such assertions before any credible proofs are made public (and continues to do so), then this question resolves as NO. If a credible proof is made public, and Gary Marcus has subsequently made such a statement, but it is still uncertain whether or not the proof is valid on Janaury 1st 2050, then this question resolves as N/A.

If a deep learning based system produces such a proof (and there are no proofs which meet the above criteria), but it is uncertain whether or not its training data has been contaminated by other work (e.g. proofs of the Riemann hypothesis published after 2024 that have entered its training data distribution), then this question resolves as N/A. If there is strong evidence that all credible proofs from deep learning systems that have been published have been contaminated by the existence of other (valid) proofs of the Riemann hypothesis, then this question resolves as NO.